
在每屆世界杯足球賽開幕之際,都會有各路大咖為大力神杯的最終歸屬“算上一卦”,其中也少不了科學家手中的數學模型。“一千個觀眾中就有一千個哈姆萊特”,十個不同模型就可能預測出十個不同冠軍,像巴西隊,阿根廷隊,法國隊都是被預測的奪冠熱門。
對于即將到來的2022年卡塔爾世界杯,英國一位流行病學統計研究者Matthew Penn卻更看好比利時隊,要知道比利時隊在世界杯歷史上還從來沒進過決賽。但這哥們絕不是在“瞎說”,一來人家有自己基于數據的概率模型,二來這個模型曾經在2020年歐洲杯的預測中大放異彩,當時準確地預測了意大利和英格蘭會分別是冠亞軍,并且預測對了八強球隊中的六個。
在11月15日,Nature雜志慕名采訪了Matthew Penn這位預測大神,并公布了他使用同一模型預測的本屆世界杯結果,各隊奪冠的可能性大小如下:
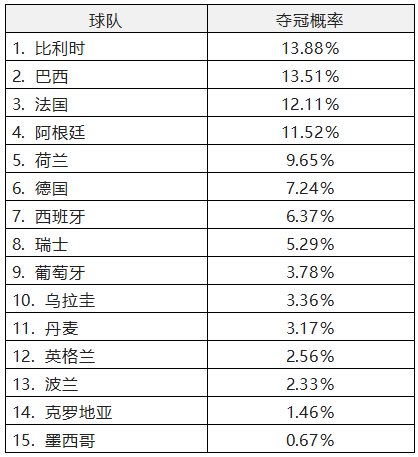
那么這些歐洲杯和世界杯的預測結果是怎么獲得的呢?簡單說是來自于每場比賽的擲骰子,卻又不是簡單的擲骰子,而是一種泊松概率分布。
我們投擲一枚普通骰子,會得到1點到6點中的任意一個,并且六種結果的可能性是相等的,稱為均勻概率分布。而對于泊松概率分布,我們考慮這樣一種情況:假設街邊有一家生意并不怎么好的小店,每天經營10個小時,平均每天可以來30個顧客,那么平均每小時就只有3個顧客,還假設顧客都是隨機選時間來的,并沒有“客流高峰”,如果任意挑選其中營業的一個小時,來的顧客人數一定是3個嗎?顯然也不一定,這次碰巧可能一個人也沒來,下次碰巧可能一下子來了十幾個人。而法國數學家泊松給出了下面這一公式:
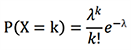
λ=3表示了平均值,P則表示了這一小時的時間段來了k個人的概率大小,e是自然常數。在泊松眼中,這家小店一小時內恰好來了3位顧客(平均水平)可能性是22.4%,而一個人沒來的概率是4.98%,來了很多人的概率同樣存在,但可能性很小,比如來了10個人的概率是0.08%,其它人數的概率也可以一一算出。
在現實中,泊松概率分布其實無處不在,很多真實數據都和這一分布驚人的相似。其中包括了核物質每秒放射性衰變的次數,地震等自然災害發生的次數,公共場所排隊的人數,機器出現的故障數,每年飛機墜毀次數,某地區患病的人數,城市各區域犯罪案件發生數量,甚至是普法戰爭期間普魯士士兵被馬踢死的人數等等。
而在Matthew Penn的模型中,泊松概率分布用來表示了每場足球比賽中某一方的進球個數。一場比賽的勝負和比分自然同時取決于雙方的實力和運氣,確定性之中又充滿了不確定性。
為了衡量各球隊實力,模型中給每一支球隊分別設置了“攻擊力”和“防守脆弱性”指數,前者數值越高越容易進球,后者數值越高表示越容易丟球,防守力越弱。對此,各種網游桌游的玩家一定不會陌生,而在更遙遠的時代,方便面里贈送的《水滸傳》英雄卡上也都標記了每位好漢的攻擊力和防御力。很顯然,一等球隊攻擊力強,防守脆弱性低,二等球隊攻擊力弱,防守脆弱性低,或者反之,最差的一類球隊攻擊力弱,防守脆弱性高。
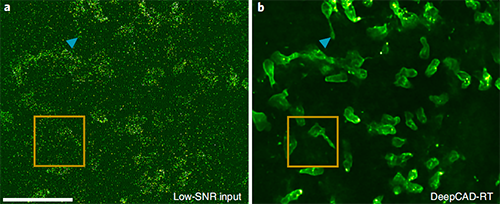
不過辦法總比困難多,就像從混亂的進球數可能性中尋找到冠軍球隊的蛛絲馬跡一樣,面對神出鬼沒的泊松概率分布噪聲,研究者通過深度學習人工智能算法可以將拍到的照片中噪聲完美去除,做到完好無缺的修復(圖右)。無論預測比賽比分,還是去除圖片噪聲,都離不開大數據作為參考,隨機性的迷霧被異曲同工地層層撥開。
作者:焦述銘(鵬城實驗室助理研究員,香港城市大學電子工程博士,從事全息三維顯示算法,單像素成像,光學計算,圖像處理,信息安全,機器學習等研究)








