理解Lambda整定方法推導的內容需要掌握拉普拉斯變換和傳遞函數等控制領域相關知識,這部分知識內容超過了本文的范疇,本文直接使用了這些知識。
Lambda整定方法的推導使用了分析設計方法,基于附圖1的簡化控制框圖。
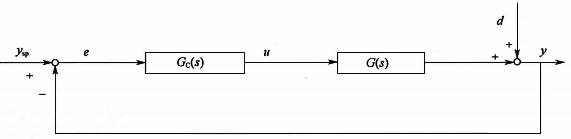
圖1 簡化的控制框圖
主通道閉環傳遞函數(公式1):

控制器傳遞函數(公式2):

1、自衡對象Lambda整定方法推導
被控對象傳遞函數(公式3):

閉環控制不能消除純滯后時間,所以設閉環傳遞函數仍有不變的純滯后時間。閉環時間常數λ表示設定值階躍變化時過程的響應速度。期望的閉環傳遞函數(公式4):
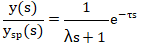
將公式4代入公式2,得公式5和公式6:
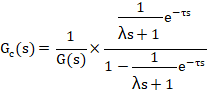
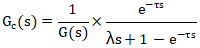
將公式3代入公式6,得公式7:
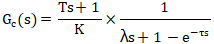
對公式7中的純滯后時間使用一階泰勒展開近似,得公式8、公式9:
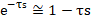

故得公式10:
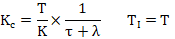
從正文我們知道,即使被控對象并不是一階純滯后對象,仍可以通過在響應曲線中獲得一階純滯后控制模型參數,得到可以實現穩定控制的PID參數,而且λ仍可以反映閉環控制性能的快慢并遵循λ≥τ。
下面分析λ的選擇原則分析。
使用Lambda整定公式后的閉環傳遞函數為公式11:
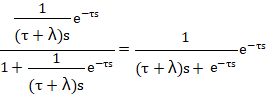
對分母純滯后進行一階Padé近似得公式12:
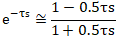
閉環傳遞函數近似為公式13:

當λ=τ,閉環傳遞函數為公式14:
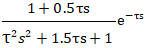
典型二階系統為公式15:
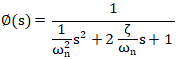
不同ξ時二階系統的階躍響應曲線如附圖2所示。公式14對應的參數得公式16和公式17:
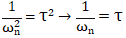
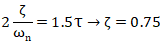

圖2 不同ξ時二階系統的階躍響應曲線
所以當λ=τ,閉環的設定值跟蹤會發生超調。此時閉環傳遞函數并不是期望的一階純滯后響應,這是純滯后的近似造成的,這也是Lambda整定方法推薦的最強控制作用。同理,當λ=2τ時,閉環設定值跟蹤不振蕩。
2、積分對象Lambda整定方法推導
被控對象可以用積分純滯后對象描述,傳遞函數為公式18:

閉環控制不能消除純滯后時間,所以設閉環傳遞函數仍有不變的純滯后時間。閉環時間常數λ表示設定值階躍變化時過程的響應速度。期望的閉環傳遞函數為公式19:
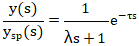
將閉環傳遞函數公式19代入方程式2,得公式20和公式21:
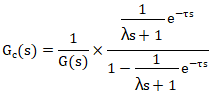
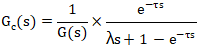
將模型公式18代入公式21,得公式22:

對純滯后使用一階泰勒展開近似,得公式23:
PID控制器傳遞函數近似為公式24:

對積分純滯后對象使用純比例控制就能滿足主通道的控制要求,得公式25:

積分對象的比例增益計算公式和自衡對象類似,λ反映了閉環控制性能的快慢。λ的選擇依據和自衡對象的推導過程一樣,這里不再贅述。所以也有結論:當λ=τ時,閉環的設定值跟蹤會發生超調。這也是Lambda整定方法推薦的最強控制作用。同理當λ=2τ時,閉環設定值跟蹤不振蕩。
3、積分對象純比例控制
實際情況中,干擾可能具有和被控對象一樣的積分特性。例如水箱或儲罐的進出流量對液位都有積分特性。如圖3所示。
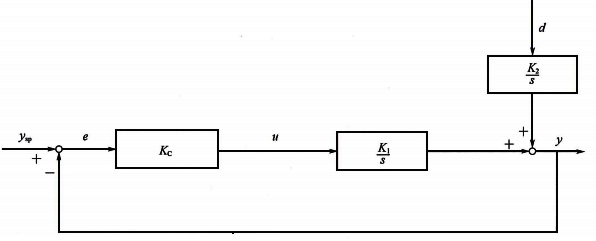
圖3 積分對象的純比例控制
擾動到過程變量的閉環傳遞函數為公式26和公式27:


此時對純積分對象的擾動通道而言,干擾會導致系統產生余差。隨著比例作用增強,余差逐步減小。
即使被控對象是積分對象,考慮到擾動的復雜性,為了消除余差,也推薦使用比例積分控制而不是純比例控制。
關鍵是積分時間如何設置才能既避免振蕩,又能消除余差。當然積分時間太大不會振蕩,但是消除余差的能力會比較弱。
4、積分對象比例積分控制
圖4中針對積分對象使用比例積分控制。
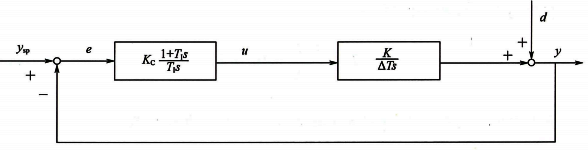
圖4 積分對象比例積分控制
傳遞函數為公式28~公式30:
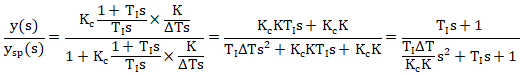
閉環傳遞函數的兩個極點位置決定了被控對象是否振蕩。根據韋達定理,極點的位置取決于根的情況由判別式(△=b2-4ac)決定,當判別式大于等于0方程式有兩個實根時,被控對象階躍響應不振蕩,否則方程式有兩個共軛虛根,被控對象階躍響應振蕩,得公式31和公式32。
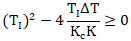
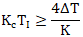
對純積分對象而言,當使用比例積分控制時,Kc或者TI足夠大使得兩者的乘積大于某個值,則積分對象比例積分控制的閉環系統都不會振蕩。當比例增益減小時,積分時間要加大才能保證閉環系統不振蕩,當比例增益增加時,積分時間即使適當減小閉環系統也不會振蕩。這是積分對象和自衡對象的顯著區別。但是純積分對象的閉環響應無論如何都會出現超調,這個超調是由閉環傳遞函數的零點造成的。
推薦的不振蕩積分時間為公式33:
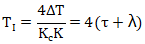
基于上面的分析,積分對象Lambda整定方法推薦參數為公式34:
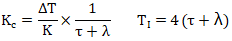
為了克服積分對象純比例控制有余差而引入積分作用后的Lambda整定方法,是對理論方法的工程化處理。工程化處理后的積分對象Lambda整定方法中λ仍然可以反映閉環響應速度,但是實際的閉環響應就不是期望的一階純滯后響應,而是始終都有超調的響應。







