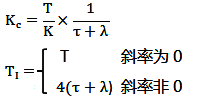在初始穩態條件下做開環階躍測試。將PID控制器的輸出(OP)進行幅度為△OP的階躍改變并保持,過程變量(PV)將會發生改變并最終穩定變化。這種描述系統或過程中輸入與輸出關系的曲線稱為“過程響應曲線”。在許多領域,都使用響應曲線進行分析和優化過程的性能。
觀察過程響應曲線,當該曲線隨著時間按照固定斜率變化時,表示過程變量的動態過程結束,可以結束開環階躍測試。
階躍響應曲線如圖1所示。取開環階躍測試開始的坐標(時間點,過程變量值)為“初始點”,過程變量以固定斜率變化之后的任一坐標(時間點,過程變量值)作為“對角點”,建立一個矩形。工業中自衡過程變量常常以固定0斜率穩定變化。矩形的上下邊距離為△PV。
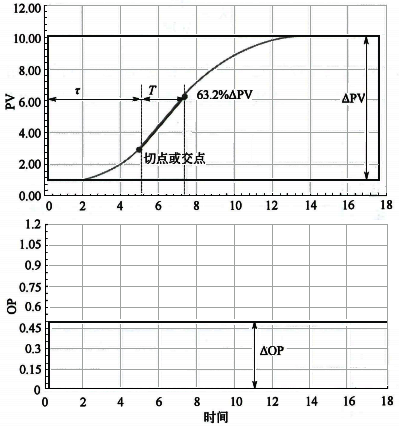
圖1 基于響應曲線的控制模型辨識工程方法1
為了描述被控變量的主要動態過程,我們需要確定響應曲線第一次到達63.2%△PV的位置。從“初始點”到該位置的時間是等效純滯后時間和等效時間常數的總和。現在要將這個時間段分割為等效純滯后時間和等效時間常數。從響應曲線第一次到達63.2%△PV的位置出發,沿響應曲線向初始點方向作響應曲線的切線或交線,切點或交點就是分割點。如果是一階模型,分割點會在矩形的底邊;如果是多容模型,分割點會在響應曲線上。
初始點到分割點的時間為等效純滯后時間τ,分割點到63.2%△PV的時間為等效時間常數T。系統等效純滯后時間一般包括真實純滯后時間、反向時間、小時間常數時間等。
如果是一階對象,交點會在實際純滯后時間,此時等效純滯后時間等于實際純滯后時間,等效時間常數等于實際時間常數。如果是多容對象,則會和響應曲線相切,此時等效純滯后時間大于實際純滯后時間。等效純滯后時間和等效時間常數的總和不變,在參數估計中,為了增加魯棒性,傾向于高估等效純滯后時間,低估等效時間常數。
等效模型增益:
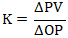
工業中積分過程變量以固定非0斜率穩定變化,也可以使用上面的類似方法進行工程辨識。階躍響應曲線如圖2所示。矩形的上下邊距離為△PV。
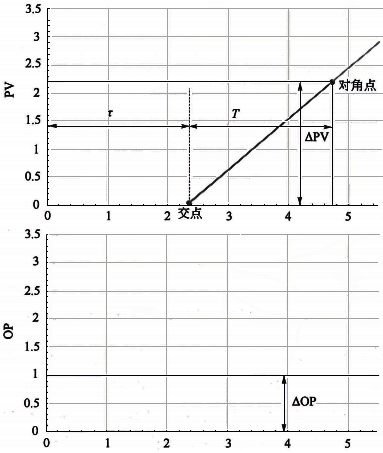
圖2 基于響應曲線的控制模型辨識工程方法2
此時,從“初始點”到對角點的時間是等效純滯后時間和等效時間常數的總和。現在要將這個時間段分割為等效純滯后時間和等效時間常數。從對角點的位置出發沿響應曲線向初始點方向作響應曲線的切線,切線與矩形的底邊的交點為分割點。
初始點到分割點的時間為等效純滯后時間,分割點到對角點的時間為等效時間常數T。系統等效純滯后時間一般包括真實純滯后時間、反向時間、小時間常數時間等。
此時Lambda整定方法可以合并為: