用時髦的話來講，正態(tài)分布是一個“高性價比”的思考工具，因為它簡單易學且應用廣。正態(tài)分布廣泛存在于自然界、社會科學、人文科學等領域，比如動物骨骼大小、考試成績、產(chǎn)品質(zhì)量指標、農(nóng)作物產(chǎn)量等數(shù)據(jù)分布大多符合這一規(guī)律。在統(tǒng)計推斷中，它是最重要的一類概率分布，也是許多統(tǒng)計方法的理論基礎。
正態(tài)分布的背景知識
平均值、方差、標準差三個部分如同土壤，會很大程度影響正態(tài)分布這棵樹的生長情況。因此，在介紹正態(tài)分布前，筆者需要簡單介紹平均值、方差、標準差。
由于樣本量的不同，平均值、方差、標準差可以分“總體”和“樣本”兩類。為強化對比，在后文的介紹中，筆者會在它們前面加上限定詞，即“總體”或“樣本”。如果沒有限定詞，那么平均值、方差、標準差所指代的就是總體的平均值、方差、標準差。
1、平均值
平均值(平均數(shù))是的小學舊識。溫故知新，因為它會在新情景下返場，用簡潔、嚴謹、優(yōu)美的數(shù)學語言，一句話回顧平均值：平均值是一組數(shù)據(jù)中所有數(shù)據(jù)之和再除以這組數(shù)據(jù)的個數(shù)，用于表示一組數(shù)據(jù)的集中趨勢。例：1和10的平均值是這樣計算的：(1+10)/2=5.5。
在正態(tài)分布中，由于樣本量不同，平均值又可以分為總體平均值(μ)和樣本平均值(
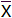)兩類，兩者的計算方法是一樣的，只是符號有差異。【小貼士】希臘字母“μ”，發(fā)音為mu，是代表總體平均值的符號；“
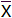”這個符號念作“X bar”，用于代表樣本平均值。2、方差
方差是衡量一組數(shù)據(jù)波動大小的統(tǒng)計量。我們學習方差最重要的，不在于掌握繁雜的計算，而是能夠根據(jù)其結(jié)果，了解所有數(shù)據(jù)的狀態(tài)。
方差分為兩類：總體方差和樣本方差。兩者的基本思路一致，但最大的差別在于樣本量不同，前者是整體，后者是整體中的部分。
若X1，X2，X3......Xn的平均數(shù)為μ，則總體方差可表示為：
【小貼士】希臘字母“ ∑” 的小寫形式為“σ”，英譯音為Sigma，大小寫符號都念“西格瑪”。圖片表示從1到n的多項求和。
我們還是用上面的1和10兩個數(shù)字，總體平均值μ=5.5的簡單例子，來看總體方差公式如何使用。(少量數(shù)據(jù)好計算，數(shù)據(jù)多的話，就讓計算機/器幫忙吧。)
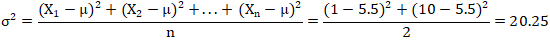
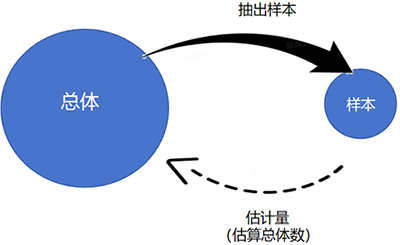
回到總體方差和樣本方差區(qū)別的話題，這里舉個簡單的例子來說明。假設我們想知道中國人身高的標準差，但因人、財、物力有限，我們不可能把所有人都量一遍，因此，只能退而求其次，采取抽樣策略，用樣本標準差來推測整體，這時，我們就會用到樣本方差。
樣本方差和總體方差計算上略有區(qū)別，主要體現(xiàn)在分母上。不同于總體方差的分母為n，樣本方差的分母為n-1。這里“-1”是為了修正樣本方差對總體方差的估計偏差，這種現(xiàn)象被稱為“貝塞爾校正”(Bessel's correction)。
這個減去的“1”，不特指任何一個數(shù)，它代表那個失去“獨立客觀”的維度(自由度)。
樣本方差的計算公式如下：
因此，在計算樣本標準差(S，即樣本方差開根號)時，其分母也是n?1而不是n(即樣本大小減1)。這里在后文標準差的部分還會提到。
【小貼士】樣本標準差的分母為什么為n-1在數(shù)學領域已被證明，是較復雜的內(nèi)容，這里不做過多展開，有興趣的讀者可查閱相關資料。
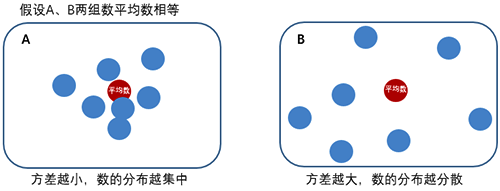
在公式的應用過程中，你或許會覺得計算很麻煩(事實也確實如此)。好消息是，計算在方差中并不是最重要的，我們要做的，是關注總體方差(σ2)的值，并由此了解方差想告訴我們的秘密：數(shù)據(jù)內(nèi)部的狀態(tài)如何。
在投資分析中，尤其是在股票投資中，方差是一個有用的統(tǒng)計工具，它可以幫助投資者了解投資組合的風險水平。同樣的回報率，方差越小，則風險越低。
3、標準差
標準差(Standard Deviation)是方差的算術(shù)平均數(shù)的平方根，也用于反映一個數(shù)據(jù)集的離散程度。標準差實際上就是方差開根。
整體標準差用σ表示，樣本標準差用S表示。兩者的公式如圖：
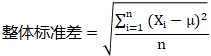
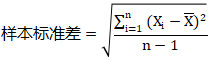
在本小節(jié)的末尾，我們來做個平均值、方差、標準差在“總體”和“樣本”符號系統(tǒng)區(qū)別上的總結(jié)。詳見下表：
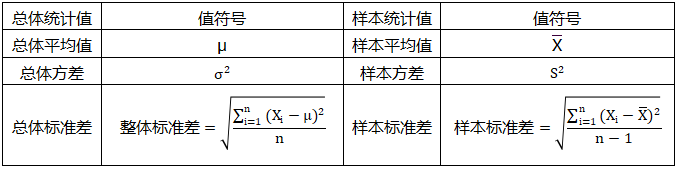
當我們談論一個正態(tài)分布時，通常是在談論一個總體的分布，而不是一個樣本的分布。因此，使用μ來表示正態(tài)分布的均值是合適的。
均值、方差、標準差的背景介紹已結(jié)束。別走開，下節(jié)更精彩，主角正態(tài)分布閃亮登場。
正態(tài)分布的主干知識
1、正態(tài)分布
正態(tài)分布一種常見的連續(xù)概率分布，它在自然科學和社會科學中常用于表示未知的隨機變量。若隨機變量X服從一個數(shù)學期望為μ、方差為σ2的正態(tài)分布，則記為N(μ，σ2)。
正態(tài)分布的曲線呈鐘型，因此人們又經(jīng)常稱之為“鐘形曲線”。正態(tài)分布雖有無數(shù)種形態(tài)，但仍由μ(平均值)和σ(標準差)兩個數(shù)值決定。其中，μ決定了正態(tài)分布的位置，σ決定了分布的幅度。理解了這一點，你就不需要單獨記憶每一個正態(tài)分布圖啦。
現(xiàn)在，讓我們一起來看一些有代表性的正態(tài)分布圖吧(下面的文字濃度有點高，值得多看幾遍)：
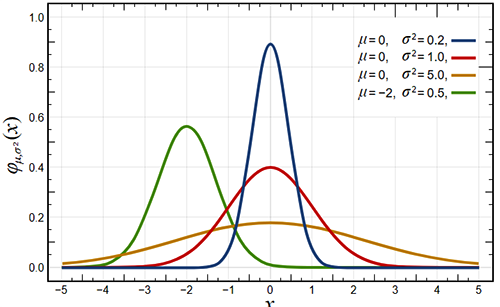
①當μ=0，σ=1時，這個正態(tài)分布就是標準正態(tài)分布，(見下圖紅線)。
②以正態(tài)分布為參考標準，μ為負則圖形向左移動(見下圖綠線)，反之，μ為正，則圖形向右移動。
③μ不變，σ越小，則正態(tài)分布曲線越陡峭(見下圖藍線)，圖像越“高瘦”，反之則越平緩(見下圖黃線)，圖像越“矮胖”。
【小貼士】不知道你是否注意到，和各行業(yè)一樣，數(shù)學也有自己的業(yè)內(nèi)術(shù)語，比如正態(tài)分布定義里的“服從”和“期望”。
數(shù)學語言中的“服從”是指“符合”、“遵從”的意思，一般指事物符合數(shù)學中的發(fā)展規(guī)律。
另外，數(shù)學術(shù)語中，“期望”或“數(shù)學期望”是一個重要的概念，特別是在概率論和統(tǒng)計學中。它表示隨機變量的預期值或平均值。
除了上面的例子，正態(tài)分布其實還有數(shù)種形態(tài)，但它們的模型主要由μ(平均值)和σ(標準差)兩個數(shù)值決定。
介紹了決定正態(tài)分布曲線的關鍵參數(shù)后，我們再來看看關于曲線下方覆蓋面積呈現(xiàn)的規(guī)律。在距離平均值±1的標準差(即±σ)范圍內(nèi)，集中著約全體68.26%的數(shù)據(jù)；距離平均值±2的標準差(即±2σ)，集中著約95.45%的數(shù)據(jù)；距離平均值±3的標準差(即±3σ)，包含著99.73%的數(shù)據(jù)。曲線下方覆蓋的面積，在統(tǒng)計學上被稱“置信區(qū)間”。
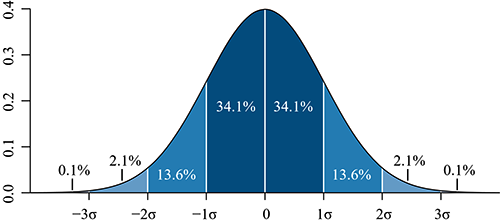
這張圖是不是有點抽象？舉幾個例子，讓置信區(qū)間中的數(shù)字走進生活。
①有大約68%的可能性，動態(tài)范圍不超過平均值±σ。在一個班上，一班的平均分為80分，如果標準差為5分，我們就有68%的置信度說，考慮到隨機性的影響，這個班的平均成績應落在75~85之間，而不是之外。
②有大約95%的可能性，動態(tài)范圍不超過平均值±2σ，即兩個σ的置信度是95%。做科學試驗時，通常需要有95%的置信度，才能得到大家認可的結(jié)論；在產(chǎn)品質(zhì)檢中，可以通過抽樣檢測來估計產(chǎn)品的平均質(zhì)量水平，并利用95%置信區(qū)間來評估這個估計的可靠性。
③如果我們進一步擴大誤差范圍到±3σ，那么這個置信度就提高到99.7%。在要求極高的實驗中，我們甚至會要求達到99.7%的置信度，甚至更高；在招聘中，面試官可以使用3σ原則來確定錄取分數(shù)線。通過計算應聘者的平均分數(shù)和標準差，可以確定一個合理的分數(shù)線范圍，從而篩選出合格的應聘者。
【小貼士】總體正態(tài)分布圖vs樣本正態(tài)分布圖(符號區(qū)別)
正態(tài)分布的標準化
在正態(tài)分布的主干知識中，我們介紹了影響正態(tài)分布形態(tài)的土壤(平均值、方差、標準差)，以及由此長出的小樹(正態(tài)分布的圖像)。
1、標準化與查表求概率
雖然通過觀察圖也能把握大致情況，但計算數(shù)值后會更便于理解，也方便向他人展示。好消息是，Z轉(zhuǎn)換(標準化)可以實現(xiàn)統(tǒng)一尺度。
對于數(shù)據(jù)集中的每一個數(shù)值X，可使用以下公式進行標準化：
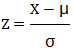
在這個公式中，Z是轉(zhuǎn)換后的標準值，X 是原始數(shù)據(jù)點的值，μ是原始數(shù)據(jù)的平均值和σ是原始數(shù)據(jù)的標準差。
別被公式嚇到，放進日常的簡單應用場景就豁然開朗了。
小A參加了小學模擬考試，數(shù)學得了73分，英語得了76分。數(shù)學平均分是60分，英語平均分是68分。那么，小A的數(shù)學成績和英文成績，哪一個相對來說比較好呢？(得分均按照正態(tài)分布)實際上，僅這些條件是無法進行判斷的，還需要能夠表示全體離散程度的標準差。現(xiàn)在，我們假定數(shù)學是標準差為8分的正態(tài)分布，英語則是標準差為6分的正態(tài)分布。
用Z變換的公式可得：
數(shù)學 : (得分-平均分)÷標準差=(73-60)÷8=1.625
英語 : (得分-平均分)÷標準差=(76-68)÷6=1.333
也就是說，當標準差為1時，小A的數(shù)學、英語成績標準差分別是1.625、1.333。不同學科的成績轉(zhuǎn)化為標準得分后，變得可比較了。
另外，用“標準得分=1”進行了標準化，“平均值”會變成什么樣呢？本來，平均分根據(jù)科目的不同而不同，但以標準得分進行分布的時候，平均值為0。
因此，在對成績進行“標準化”時，分布會變?yōu)槠骄?0、標準差=1的標準正態(tài)分布。需注意的是，標準化改變的只是圖的位置，比如向左或向右平移，但并不會改變“高矮胖瘦”。
完成Z變換，我們就通過可以利用z值表找到對應的概率值啦。這里會用到“標準正態(tài)分布表”。
這個表是前人整理好的數(shù)據(jù)，用起來也很方便。首先，我們要看最左手列，去查閱Z至小數(shù)點后1位數(shù)，之后，我們再查最上一行，看Z的第二位小數(shù)，左右交叉得到的數(shù)，就是我們需要找的數(shù)。
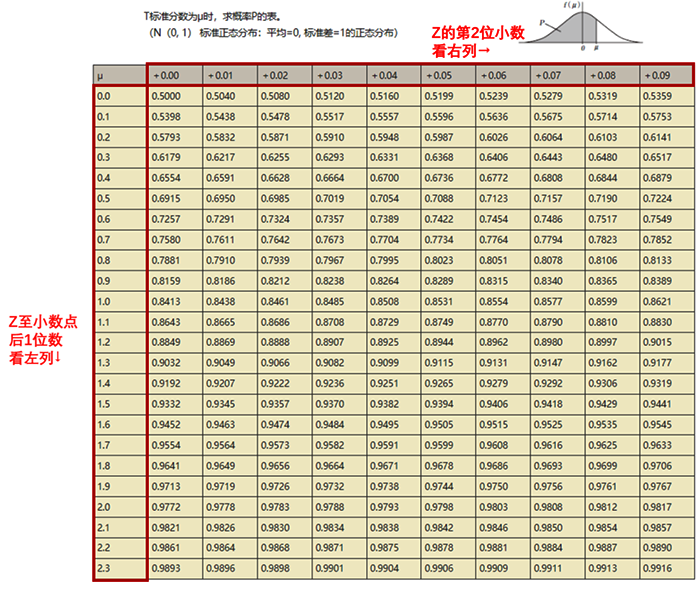
放到小A的例子中，數(shù)學的標準差為1.625、英語的標準差為1.333。我們來試試查這個表。以數(shù)學為例，先看最左列，Z至小數(shù)點后1位數(shù)為1.6，接著，再看最上行，Z的第2位小數(shù)我取0.02，交叉得到的數(shù)就是0.9474(藍色方框中的數(shù))。英語的查閱方式同理，取值為0.9082。
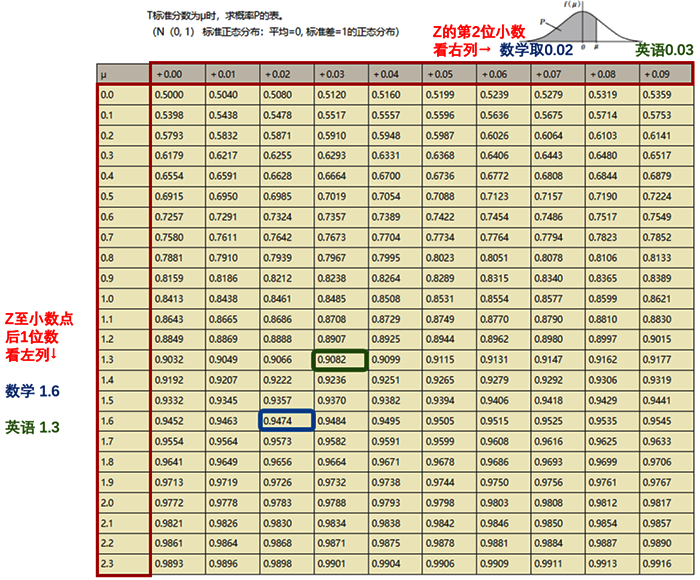
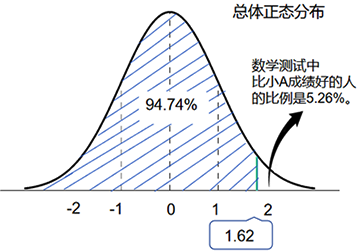
查表后，就是分析數(shù)據(jù)了。數(shù)學取值為0.9474，英語為0.9082，即數(shù)學約處于94.74%的水平，英語處于90.82%的水平。如果參加全國數(shù)學、英語模擬考試的人有1萬人，小A數(shù)學大概處于526名的位置((1-0.9474)×10000=526名)，英語處于918名的位置。用圖表示更清晰，這里以數(shù)學為例：
恭喜看到這的你，在20分鐘左右的時間，你已經(jīng)了解了正態(tài)分布最核心的知識！
最后，請讓我們?yōu)槟阕鰝€簡要的總結(jié)：我們先一起回顧了平均值、方差和基本差的背景知識，并在此基礎上了解了正態(tài)分布的形狀、特征以及如何使用。
