
傅里葉級數和傅里葉變換背后的基本思想
傅里葉級數和傅里葉變換背后的直覺是相同的:任何函數都可以寫成正弦函數之和。
這個想法如此簡單,卻又極其深刻。在高中課程中大家了解了余弦和正弦,它們將直角三角形的角度與兩條邊長之比聯系起來。另一種理解方式是,余弦和正弦分別是繞單位圓移動的點的x坐標和y坐標。它們是人們能想到的最簡單的周期函數之一。
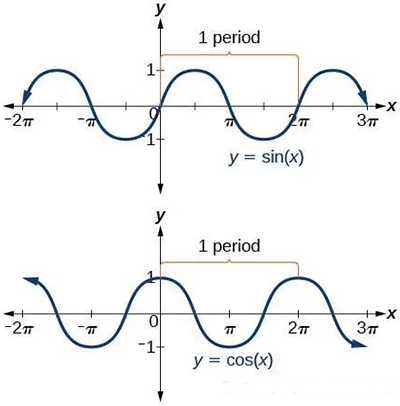
正弦和余弦函數圖
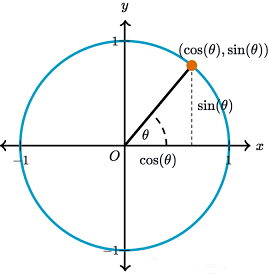
余弦和正弦作為繞單位圓運動的點的坐標由這兩個函數組成的和可以表示任何數學函數,這一事實至少讓人瞠目結舌。
但是,傅里葉級數和傅里葉變換有什么區別?傅立葉級數和傅立葉變換的區別在于,傅立葉級數用于將周期函數分解為正弦和余弦之和,而傅立葉變換則用于非周期函數。
現在讓我們來看看這兩種方法分別是如何實現這一目的的。
傅立葉級數
正如我們所說,傅里葉級數用于周期函數。作為快速提示,如果以下條件成立,則稱函數f(t)為周期函數,基本周期為T:f(t-T)=ft=f(t+T)。簡單地說,這意味著函數以長度為T的固定間隔重復其值。
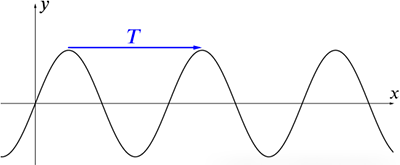
周期函數舉例
最后,我們將周期函數的基頻定義為1/T,即基頻周期的倒數。如果周期告訴我們函數重復的頻率,那么頻率則告訴我們每單位時間(或函數所依賴的任何其他單位)有多少次重復。
現在我們已經掌握了定義傅立葉級數所需的一切。
傅里葉級數是正弦函數的無限加權和,每個正弦函數的頻率都是原始周期函數基頻的整數倍(1/T)。
傅立葉級數的公式如下:
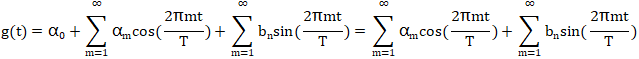
周期函數g(t)的傅里葉級數展開
初看起來有點復雜,讓我們來分解一下。
①細分
我們從基本周期為T的周期函數g(t)開始。一個是余弦和,另一個是正弦和。這兩個和都是加權的,簡單地說,就是它們所包含的每個余弦和正弦都有一個系數。在我們的例子中,這些系數分別用符號αm和bn表示。下標字母m和n是和的計數變量。因此,當m變為1、2、3等時,每個余弦的系數就會從α1變為α2,依此類推。
最后,在三角函數(余弦和正弦的另一個名稱)的內部,我們發現了自變量t(也是初始函數g(t)的自變量)、常數2π(由于與對稱性有關的原因而存在,但對本文并不重要)以及分母中的基本周期T。您可能已經注意到,我們可以用基頻f代替上式中的比率1/T,以避免使用分數。
我們在三角函數中遇到的最后一個符號是每個和的計數變量,余弦為m,正弦為n。它的作用是使無限和中的每個余弦和正弦具有不同的頻率。不過,這些頻率并非任意頻率。它們是初始函數g(t)頻率的多個整數,即f=1/T。頻率以這種方式相關的正弦被稱為諧波相關。
計算系數αm和bn的公式如下。由于它們對于我們的理解沒有什么幫助,我們就不多說了。
傅立葉級數三角函數形式的系數
我們完成了!你現在知道如何將任何周期函數展開為余弦和正弦之和了。
傅立葉級數的替代形式(可選)
在開始學習傅里葉變換之前,大家還可了解另一種表示傅里葉級數的方法,但卻是等價的。具體如下:
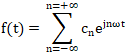

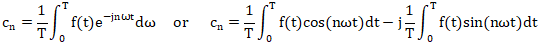
傅立葉級數的指數形式
雖然初看起來與我們上面討論的三角函數形式有很大不同,但實際上是等價的。我們所做的就是利用歐拉公式(它將余弦和正弦與復指數聯系起來),以更簡潔的形式重寫傅里葉級數。現在,我們只有一個和,而不是兩個和。
傅立葉變換
如果您已經理解了有關傅里葉級數的所有內容,那么傅里葉變換就會變得非常簡單。這次我們關注的是非周期函數。傅立葉變換的公式如下:
傅立葉變換的重要性
傅立葉變換的結果是頻率的函數。請記住,希臘字母歐米茄“ω”用來表示角頻率,它是乘積2πf的別稱。當初始函數f(t)是一個時間函數時,傅里葉變換給出了該函數的頻率內容。摘自維基百科的一句話:時間函數的傅里葉變換是頻率的復值函數,其幅值(絕對值)代表原始函數中該頻率的量,其參數是該頻率中基本正弦波的相位偏移。傅里葉變換并不局限于時間函數,但原始函數的域通常被稱為時域。
我們可以利用反傅里葉變換找回初始函數:
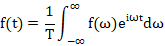
傅里葉變換和傅里葉反變換
①細分
讓我們比較一下反傅里葉變換和傅里葉級數。
首先,我們使用復指數來表示正弦函數,而不是使用余弦函數和正弦函數(這會導致兩個積分),這樣會更加簡潔。積分前的系數1/2π是為了對稱的目的。
我們馬上會注意到的另一件重要事情是,我們現在有了一個積分,而不是離散的“西格瑪 ”和。請記住,積分本身也是和,唯一不同的是,在積分下求和的量是連續的,而不是離散的。由于初始函數f(t)現在是非周期的,我們需要所有可能的頻率(從負無窮到正無窮)來表示它。在傅里葉級數的情況下,我們只使用T的整數倍。由于我們現在沒有基本周期T,我們不得不使用所有的T。
至于復指數的系數,我們可以得到該函數在每個可能頻率ω下的傅里葉變換值。正如您所看到的,從傅里葉級數的概念到反傅里葉變換的概念之間存在著明顯的一一對應關系。
結束語
正如泰勒級數將函數分解為單項式的無限加權和一樣,傅里葉級數和傅里葉變換幫助我們將周期函數表示為正弦波的加權和。正弦波是美妙的函數,在數學意義上很容易操作。如果我們知道一個系統(可以是帶彈簧的經典系統,也可以是處理信號的系統或其他任何系統)對正弦波輸入的響應,那么我們就可以利用上述思想將任何其他輸入表示為正弦波之和。這樣,分析的很大一部分就已經完成了,數學也變得簡單多了。因此,傅里葉級數和傅里葉變換在電子工程、儀器儀表、物理學和生物學等所有科學領域都有大量應用。
相關閱讀
◆傅里葉級數的發現與應用
◆什么是模擬信號、數字信號、連續時間信號和離散時間信號







