筆者利用該方法研究了單相與三相交流充電樁的需要系數、超高層建筑的變壓器容量指標等,分析過程如下。
首先應對樣本組進行壞點處理,使得數據更科學、更具代表性。一般情況下,可以先假設數據呈正態分布的規律,這里采用SPSS軟件作柯爾莫哥洛夫-斯米爾諾夫檢驗(即K-S檢驗)驗證正態分布。
◆SPSS為Statistical Product and Service Solutions的縮寫,即“統計產品與服務解決方案”軟件,由IBM公司研發。
◆К-S檢驗是基于累計分布函數,用以檢驗兩個經驗分布是否不同或一個經驗分布與另一個理想分布是否不同。
當顯著性α值大于0.05時,則上述假設成立。顯著性水平是估計總體參數落在某一區間內,可能犯錯誤的概率。
若已驗證樣本數據符合正態分布規律,可根據正態分布公式(見下式)得出樣本均值μ和標準差?。

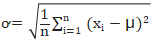
公式中,n為樣本數量;xi為樣本值,i=1,2,……,n;μ為樣本均值;?為標準差。
已知均值和標準差便可求取參考值范圍,此處采用頻數分布估計法估計任意取值范圍內的頻數比例,制定參考值范圍。頻數分布(frequency distribution)是數據統計整理方式之一。
下式中,X為雙側界值,即范圍邊界,邊界大小以顯著性水平α值來確定,即估計總體參數落在某一區間內可能犯錯誤的概率,其常用值有0.01、0.05、0.10等。鑒于需要系數是工程應用參數,實際情況比較復雜,所以不需將參考值范圍定的過小,我們取α值為0.10,即參考范圍至少能滿足10%的情況。u值的選取與參考值范圍的選擇有關,常用u值見下表。
X=μ±u?
公式中,X為雙側邊界值;u為標準正態變量。
表 常用u值

顯著性水平α取0.10,則雙側界值為P5和P95,可得:X=μ±1.645?
這樣,通過分析參考范圍的合理性,并綜合實際運行情況,即可得出需要系數建議值。







